Cam Clay
The modified Cam clay model represents a classical critical state model based on the theory of plasticity. The main features of the model are similar to the hypoplastic model for clay. Unlike the hypoplastic models the modified Cam clay model distinguishes the elastic and plastic part of strain components and therefore allows for straightforward visualization of permanently strained plastic zones. On the other hand the onset of plastic behavior and the associated change of stiffness is sudden and not gradual as in hypoplastic models.
The modified Cam clay model takes into account the following important properties of soils:
- Stiffness and strength depend on the current level of effective stress \(\boldsymbol{\sigma}\)
- Stiffness and strength depend on the current density characterized by the void ratio \(e\)
- Stiffness depends on the direction of loading (loading vs. unloading)
Model parameters
The model introduces five material parameters that are constant for all possible states of a particular soil and a state variable that evolves during straining. Thus the modified Cam clay model is different from the Mohr-Coulomb model which employs distinct values of its material parameters for the same soil in different states (loose or dense). In particular, the Cam clay model uses five material parameters:
- \(e_{0}\) - Position of the normal consolidation line
- \(\lambda\) - Slope of the normal consolidation line
- \(\kappa\) - Slope of the unloading/reloading line
- \(M_{cs}\) - Slope of the critical state line
- \(\nu\) - Poisson ratio
and one state variable, namely the preconsolidation pressure \(p_{c}\).
Parameters \(e_{0}\) and \(\lambda\)
Parameters \(e_{0}\) and \(\lambda\) define the position and the slope of the isotropic normal compression line (NCL) in the \(\ln(\sigma_m)\times e\) space as illustrated in Figure 1 (note the difference from the hypoplastic model for clay where the similar parameters are defined for NCL in \(\ln(\sigma_m)\times\ln(1+e)\) space). The normal compression line defines a theoretical response of the soil sample during isotropic compression test. Since the model assumes incompressible grains the resulting volumetric strain depends on the decrease of volume of pores only and thus on the void ratio.
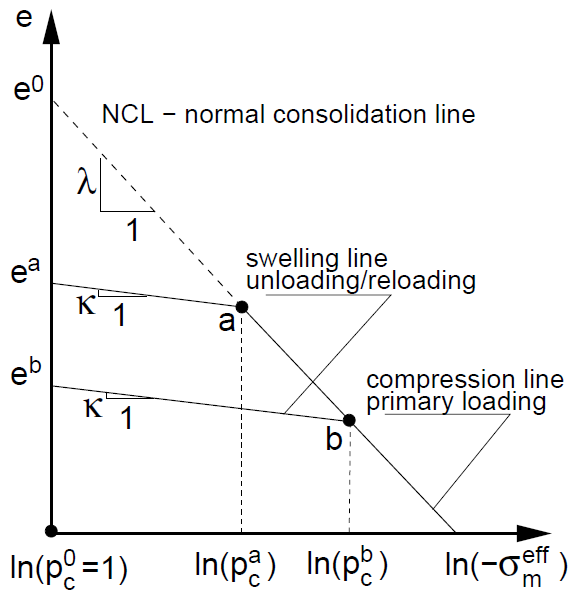
Figure 1: Normal consolidation line and unloading/reloading line assumed in the modified Cam clay model
Parameter \(\kappa\)
Parameter \(\kappa\) defines the slope of the unloading/reloading line in the \(\ln(\sigma_m)\times e\) space as illustrated in Figure 1. Unlike the NCL which is fixed vertically by parameter \(e_0\) the position of the unloading/reloading line depends on the maximal previous compression stress denoted as the preconsolidation pressure \(p_{c}\).
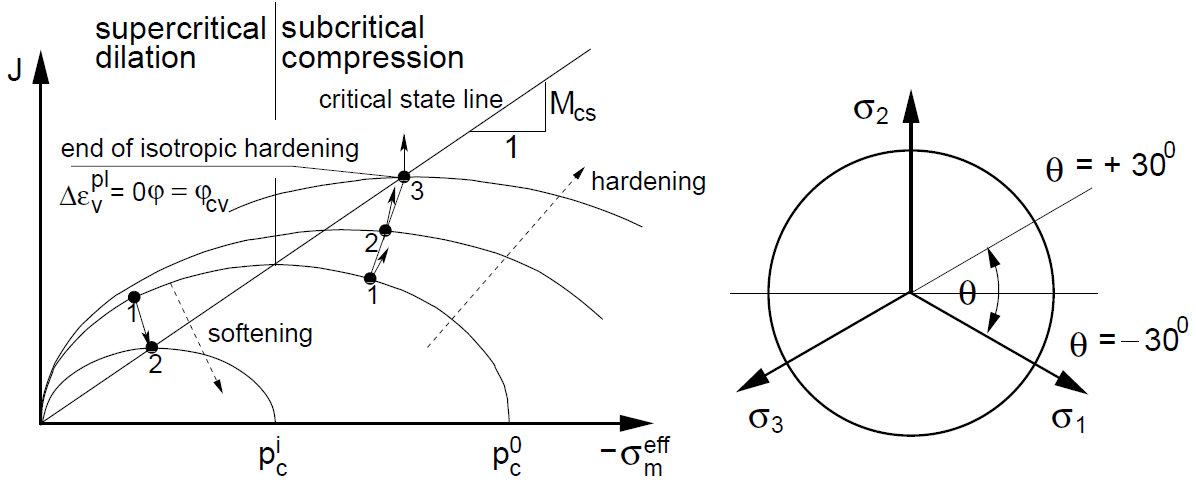
Parameter \(M_{cs}\)
Parameter \(M_{cs}\) is the slope of the critical state line plotted in the \(\sigma_m \times J\) space, see Figure 2.
The slope \(M_{cs}\) is computed from the critical state angle \(\varphi_{c}\) by \begin{equation} M_{cs} = \frac{2\sqrt{3}\sin\varphi_{c}}{3-\sin\varphi_{c}} \label{eq:Mcs} \end{equation}
Parameter \(\nu\)
Parameter \(\nu\) is the Poisson ratio known from linear elasticity. It controls the ratio of radial and axial elastic strains under uniaxial loading and consequently the ratio between the (stress dependent) bulk and shear moduli.
Preconsolidation pressure \(p_{c}\)
The model has one state variable - the preconsolidation pressure \(p_{c}\). For an isotropic compression test the preconsolidation pressure \(p_{c}\) corresponds to the maximal mean stress \(-\sigma_{m}^{eff}\) to which the soil has been subjected. The kinematics of the model is evident from Figure 1: Soil sample with an initial state \(a\) (it has void ratio \(e^{a}\) and preconsolidation pressure \(p_{c}^{a}\)) is loaded isotropically up to the compressive mean stress \(\sigma_{m}^{eff} = -p_{c}^{a}\). The deformation during this loading is nonlinear but elastic, i.e. if the soil is unloaded from this point it returns along the \(\kappa\)-line back to the state with \(e = e_{a}\) and no permanent volumetric strain occurs. If the soil is loaded beyond the point \(p_{c}^{a}\) it moves along the \(\lambda\)-line. During this loading both the elastic and the plastic volumetric strain develop. When the soil is unloaded from the point \(\sigma_{m}^{eff}=-p_{c}^{b}\) it moves along the new \(\kappa\)-line defined by the new value of preconsolidation pressure \(p_{c}=p_{c}^{b}\). As evident from the initial and final (in unloaded state) values of the void ratio \(e_{a}>e_{b}\) the permanent volumetric strain developed during this loading sequence.