Hypoplastic Clay
The hypoplastic model for clay takes into account the following important properties of soils:
- Stiffness and strength depend on the current level of effective stress \(\boldsymbol{\sigma}\)
- Stiffness and strength depend on the current density characterized by the void ratio \(e\)
- Stiffness depends on the direction of loading (loading vs. unloading)
For detailed description of the hypoplastic model calibration, see the following document. Brief description of the parameters is given below.
Model parameters
The model distinguishes between material parameters that are constant for all possible states of a particular soil and state variables that evolve during straining. In this sense the hypoplastic model is fundamentally different from the Mohr-Coulomb model which employs distinct values of its material parameters for the same soil in different states (loose or dense). In particular, the hypoplastic model for clay requires five material parameters:
- \(N\) - Position of the normal consolidation line
- \(\lambda^{*}\) - Slope of the normal consolidation line
- \(\kappa^{*}\) - Slope of the unloading/reloading line
- \(\varphi_{c}\) - Friction angle in the critical state
- \(\nu\) - Controls the value of the shear modulus
and one state variable, namely the void ratio \(e\).
Parameters \(N\) and \(\lambda^{*}\)
Parameters \(N\) and \(\lambda^{*}\) define the position and the slope of the isotropic normal compression line (NCL) in the \(\ln(\sigma_m)\times\ln(1+e)\) space as illustrated in Figure 1. The normal compression line defines a theoretical response of the soil sample during isotropic compression test. Since the model assumes incompressible grains the resulting volumetric strain depends on the decrease of volume of pores only and thus on the void ratio.
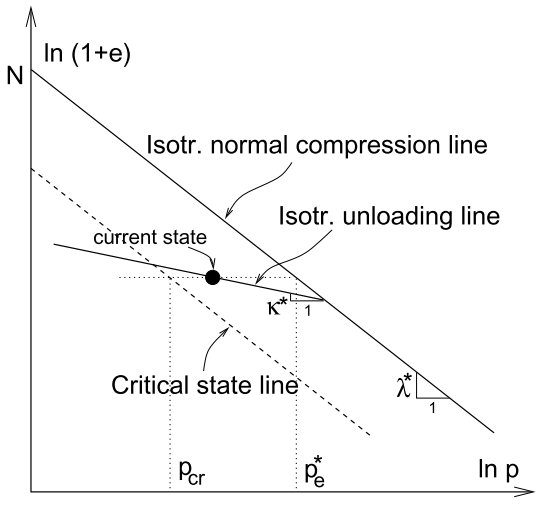
Figure 1: Normal consolidation line and unloading/reloading line assumed in hypoplastic model for clay
Parameter \(\kappa^{*}\)
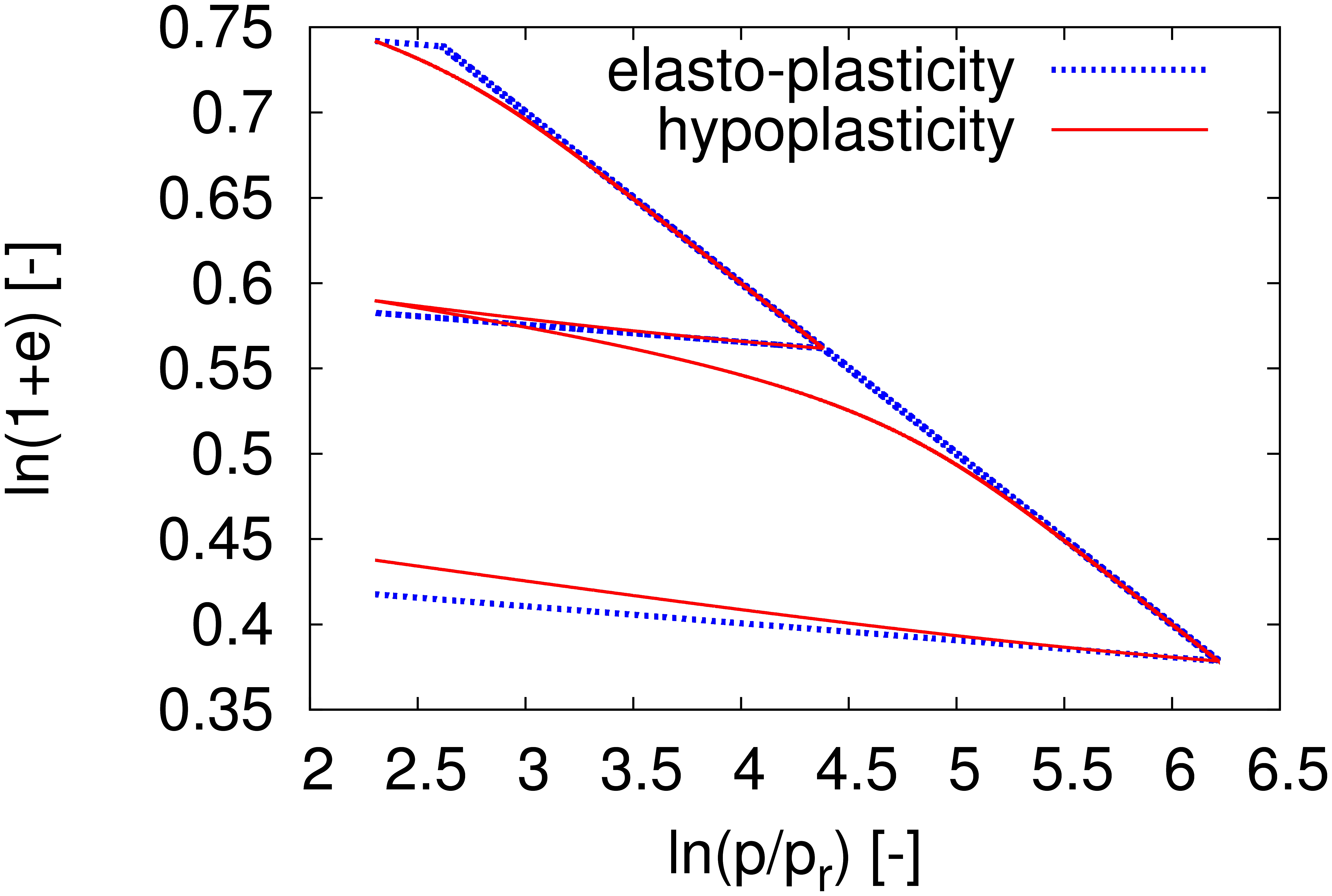
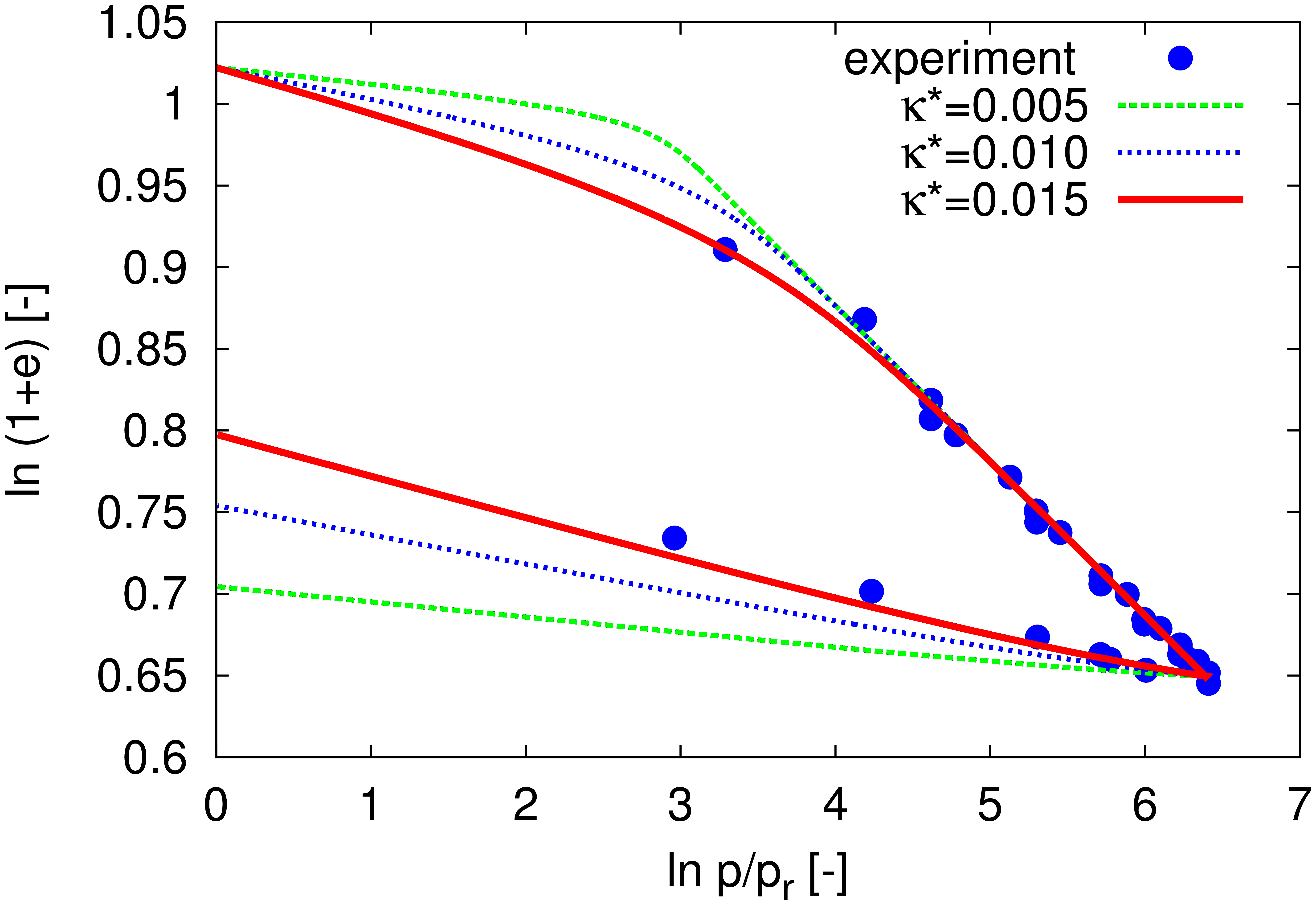
Parameter \(\kappa^{*}\) defines the slope of the unloading/reloading line in the \(\ln(\sigma_m)\times\ln(1+e)\) space as illustrated in Figure 1. Unlike the NCL which is fixed by parameter \(N\) the position of the unloading/reloading line depends on the previous compression stress. In addition, unlike simple elasto-plastic models, the slope of the unloading-reloading line is non-linear in hypoplasticity, as demonstrated in Figure 2 and 3. The parameter \(\kappa^{*}\) should thus be calibrated by means of simulation of a laboratory test, rather than by directly evaluating its slope.
Parameter \(\varphi_{c}\)
Parameter \(\varphi_{c}\) is the critical angle of internal friction. For fine-grained soils the angle of repose can not be measured and the critical friction angle has to be determined from triaxial shear test. For normally consolidated samples where no softening occurs during the triaxial shear test the critical friction angle correspond to the maximal mobilized friction angle. For overconsolidated samples the critical friction angle corresponds to the mobilized friction angle after the peak, but its estimation using these tests is often problematic (due to strain localization into shear bands and progressive decrease of strength from the peak through critical towards the residual value).
Parameter \(\nu\)
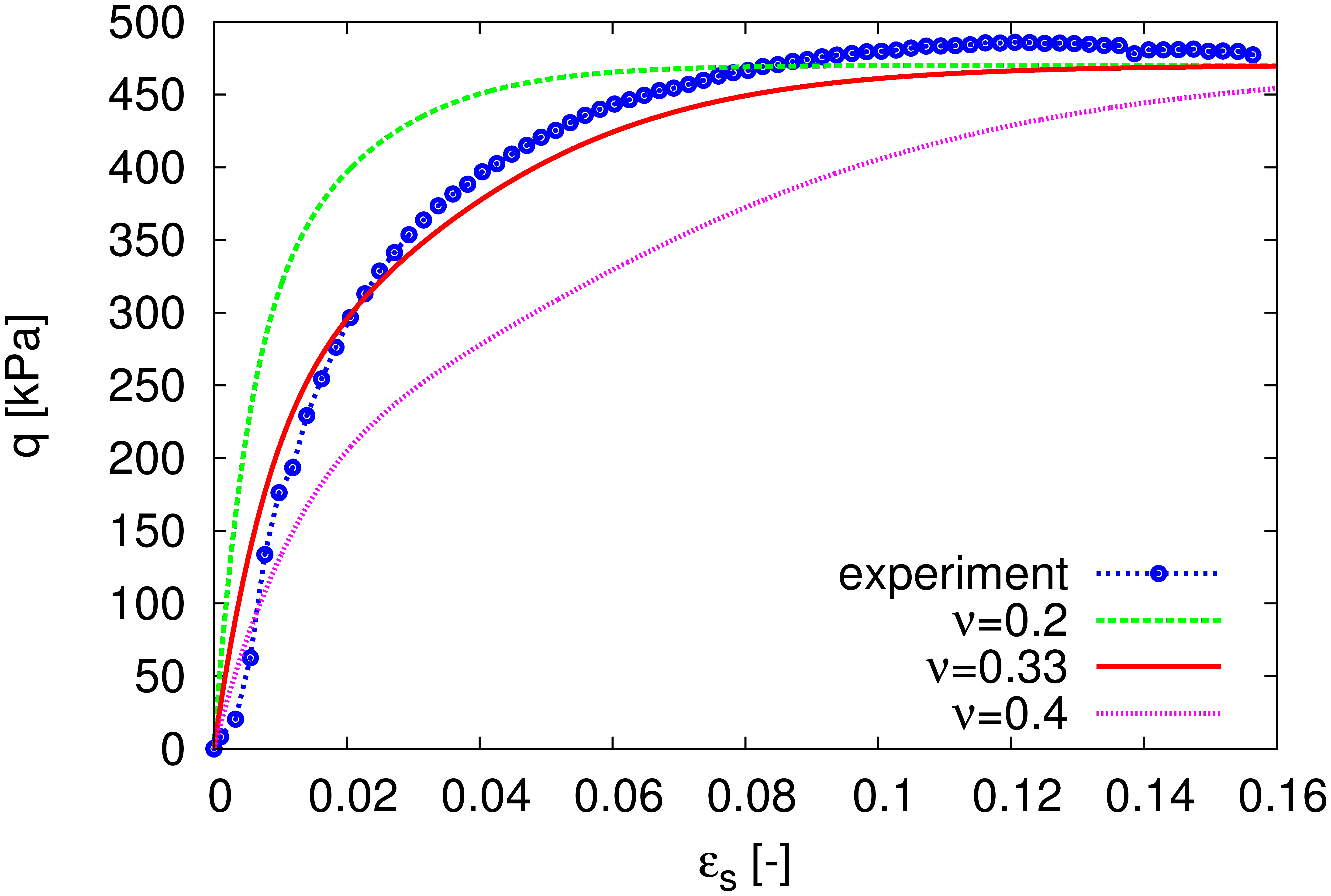
Parameter \(\nu\) controls the value of the shear modulus. In the isotropic normally consolidated state, the bulk and shear moduli are linked through the parameter ν. During shear test the shear modulus evolves non-linearly. Its magnitude being controlled by the parameter \(\nu\) and by the distance from the failure state. Example of the effect of \(\nu\) on the stress-strain curve of undrained triaxial shear test is in Figure 4.